Learning the Times Tables? Here's How to Do It - Without Tears!

The multiplication facts (or “times tables”). 

They’re important. Kids who don’t know them will struggle later in math.

But many kids resist learning these facts, complaining that they are boring and pointless. And many parents dread them, having had similar experiences as students themselves (and maybe having forgotten their math facts by the time their kids are learning them).

Let’s look at how we can apply a bit of insight from learning science to make the times tables easier to learn and remember.

What’s the problem?

The multiplication facts are usually presented in a table like the one below (the familiar “times table”). We’ll focus on the facts from 1x1 through 10x10 here.

The most common strategy for learning the facts is “brute force memorization” – which means using a combination of worksheets, drills, flashcards and the like to badger the brain into remembering this information through sheer repetition – that is, repeating the same problems over and over again. 

If the brain were like the hard drive on your computer, this might be fine. In fact, we can enter the table of numbers above into a spreadsheet and save it to our computer’s hard disk on the first try – no problem at all.

But we know from brain research that your brain is nothing like the hard drive on your computer. In fact, brute force memorization alone is probably one of the worst possible ways for a human being to learn something.  Brute force memorization can be unpleasant - no wonder kids resist it! – and it’s ineffective.  Even if you manage to hammer the information in there, it’s more likely than not to leak away pretty quickly.

There is a better way

The brain isn’t set up to store large numbers of isolated facts rapidly (like a hard drive).  Instead, it’s set up to identify and encode meaningful patterns. 

What kinds of patterns? Well, visual relationships and symmetry are two good examples. Let’s take a look.

How is the times table constructed?

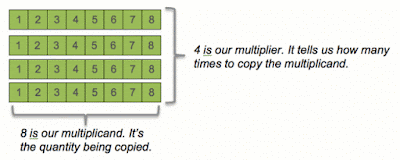
Have you ever thought about where the times table comes from? To understand that, first think about what a multiplication represents. 

If we take a multiplication like 8x4, we are saying we want to copy one number (the multiplicand) a certain number of times (the multiplier).  There’s no hard and fast rule about which order the multiplier and multiplicand are written. For our purposes, consider the first number (8) to be the multiplicand (the number being copied) and the second number (4) to be the multiplier (the number of copies). So in this case “eight times four” means “copy the number eight, four times.”  (Note that the word “multi-ply” is derived from the words for “many layers” – you can see why in the diagram below).

How do we get from the four eights to the result of the multiplication (which is 32)? Easy – just count out the number of squares in the whole rectangle like so…

The familiar times table is made up of all the rectangles representing all the multiplications from 1x1 to 10x10 laid one on top of the other, so that only the very last square of each one - containing the final count of squares in that rectangle - peeks through.  If you look at the cell for the multiplication of interest, you can see that it is at the top, right corner of a rectangle that represents the multiplication of interest (and covers that number of squares).

This visual relationship between the individual multiplication problems and the structure of the whole table can help students understand and remember the facts, because they can start to picture the problems visually in their mind’s eye. Also, if they forget one of the facts, then this conceptual understanding gives them a way to reconstruct it from known facts nearby. 

How can symmetry help students learn the facts?

Consider the multiplication 8x4=32.  This means, “copying eight squares four times gives you thirty-two squares.”  Notice that 4x8=32 means something different, namely “copying four squares eight times gives you thirty-two squares.”  The picture below shows the two visually. 

The rectangles represented by the two multiplications are different shapes, but they give the same result in the end (32 squares).  This works for any two numbers you multiply – changing the order changes the rectangle’s shape but doesn’t change the quantity that results.  This is called the commutative property of multiplication. 

Now let’s apply this insight back to our times table. Look at the table below.  It’s the same as the one above, but color-coded to highlight the symmetry associated with the commutative property. Notice that if you folded the table on its diagonal, the numbers in the two halves would overlap perfectly.

For students, this is great news – it means instead of memorizing all 100 facts, they can learn 55 facts (45 facts in one of the triangles plus the ten facts along the diagonal that are perfect squares like 1x1 or 4x4 – on the diagonal the multiplicand and multiplier are the same and so they have no mirror image).  Learning this one relationship cuts the number of facts almost in half instantly. 

Multiplying by 1: Mono-plying

We can cut the number of facts down further by looking at specific groups of facts.  Multiplying by one, for example, is not really multiplying at all – it’s mono-plying (if multi-ply means “many layers” then mono-ply means “one layer”). 

Remembering the mono-plying rule (multiplying any number by 1 gives you back that same number) takes care of another ten facts, leaving us with just 45 facts to learn.

Multiplying by 10

Multiplying tens is easy, too.  It’s just like multiplying by one except you append a zero to the result.

2x1 = 2 and 2x10 = 20 = “twenty” (derived from the words “twin tens”)
3x1 = 3 and 3x10 = 30 = “thirty”   (derived from the words “three tens”)
4x1 = 4 and 4x10 = 40 = “forty”    (derived from the words “four tens”)
and so on…

To see why, look at the picture.

Adding the rule for multiplying tens takes care of another nine facts, leaving just 36 to learn. 

If 36 multiplication facts still seems like a lot, consider that there are 26 letters in the English alphabet plus ten digits that have names (zero, one, two, etc.), which is also 36 facts.  Your child memorized those, and you can use the same kinds of techniques for the remaining 36 times table facts.  Just keep in mind that helping a child to understand where the facts come from along with patterns like the visual relationships between rectangles and the symmetry that comes from the commutative property will make learning the facts (and other things later, like long multiplication, division, and algebra) much easier.  The knowledge will also stick better and last longer.

Summary

To summarize, we started with 100 multiplication facts to learn, from 1x1 through 10x10. 

First we introduced a few key concepts:

• What is multiplication? It’s copying one number a specified number of times (as in “eight times four” and “times table”) and counting up the quantity that results
• Where does the times table come from? From stacking all the multiplication rectangles on top of one another, letting just the last square of each with the total quantity for that rectangle show through

Then we introduced a few key rules:

• Commutative Property: It doesn’t matter which order you multiply two numbers – it means something different but you still get the same result (Example: 8x4 = 4x8 = 32)
• Multiplying by one (or mono-plying): When you multiply any number by one, you just get that number back
• Multiplying tens: Just like multiplying by one, except you append a zero to the result (Example: 1x4 = 4 and 10x4 = 40). Remember: the name “forty” is just a short form of “four tens”

With these few rules we cut down the number of facts to a manageable 36. Not only does this reduce the memorization load by about two-thirds, but the conceptual understanding will make the remaining facts easier for students to learn and remember.

Additional resources

This is a lot of information (who knew there was so much to know about the lowly times tables?).

Some teachers, tutors, and parents can make use of it in the form it’s presented here in the blog post. To make it easier for everyone else, I’ve packaged this information up into some free videos and a couple of inexpensive apps for iPhone and iPad - each priced less than a pack of index cards. (Note: If you are searching for one of the apps on an iPad, you'll need to change the default filter from "iPad" to "iPhone" apps to find them).

Another great way to help kids learn is to insert yourself into the process – show them you’re interested and available to help if they need it. The same way you read books to your children when they were small, you can sit with them and work through some math mini-lessons at the table, in Minecraft, or using these apps.

Video examples of using Minecraft to learn arithmetic:

• Minecraft Math #1: Numbers - Even, Odd, Prime & Square Root
• Minecraft Math #2: Addition, Multiplication & Commutativity

Bognor’s curse – An Interactive Educational Mini-Adventure

Something’s gone terribly wrong at the Ministry of Magic. The evil wizard Bognor has cast a terrible curse across the land and it’s up to you – a lowly apprentice – to defend your village and defeat his dark magic. To succeed, you’ll have to master some basic Arithmancy. Will you do it?
Watch the video
Experience the magic

Multiplication Explained – Master the Times Tables with Understanding

Multiplication Explained is more than a typical flashcard app. It is a complete mini-curriculum designed to promote both conceptual understanding and fact fluency at the same time.  

Watch the Video
Get the App

Comment and share!
I always love to hear from parents, teachers, and students about ways I can make these resources more useful to help you learn and teach, and what other topics you would like to explore in the blog. 

Educational Assessment: A Huge Waste of Time and Money?

An educational road trip

Imagine it’s 1980 - no World Wide Web, no cell phones, no GPS. Your child is learning to drive a car. They have to drive from Los Angeles to New York in time to attend an important event that could well influence the course of their future life. How would you help them do it? They’d need a long-range plan, of course – a map with a route marked out on it. But this plan alone wouldn’t get them there – they’d need to actively interpret the directions in the real world – identifying which of the many small streets is the right one to turn on, looking for signs and landmarks to know when to change lanes and prepare to exit the highway, constantly checking to make sure they didn’t take a wrong turn, and figuring out how to get back on track when they inevitably do. They must, in other words, constantly be assessing the situation – determining where they are on the map, where that puts them in relation to the route, and what to do at each moment to stay on track and on schedule.

This driving scenario is analogous to formal education. In this case, the subject matter (arithmetic, world history, etc.) is the map. The curriculum is the route marked out on the map. The student is the driver.  The assessment is the process of tracking location and progress in relation to the route, destination, and schedule.

What’s missing from this picture?

If you are a parent, this scenario might make you feel uneasy. Would you really be ok having your child learn to drive while also following a complex and unfamiliar route across thousands of miles over a number of days with important consequences riding on their timely arrival? (Analogously, would you expect that your child would buckle down and successfully learn to read books or master algebra on their own by June, given that they want to be a writer, carpenter, engineer, doctor, or architect when they grow up?) Probably not. If they had to make the trip by car and they had to do the driving, you’d probably want to send someone along with them – a navigator and guide who knows the route well, can coach them on how to drive safely and skillfully, and looks after their well-being during the trip - making sure they leave on time each morning, get plenty of sleep, and don’t get lost or sidetracked visiting roadside attractions along the way.

In the educational analogy, the navigator is the educational guide.  But not a classroom teacher – this navigator is a personal tutor working with one student.

Imagine that we cannot afford to provide a navigator (personal tutor) for each driver, but that we can allocate one navigator for each fleet of twenty-five cars. These cars are all leaving from different starting cities, at different times, moving at different speeds, with drivers who have different levels of driving experience and skill, and different levels of familiarity with their route.  Nonetheless, the fleet navigator is responsible for seeing that all drivers arrive in New York within the same hour.

In the educational analogy, the fleet navigator is the classroom teacher.  The cities the students start in are their prior knowledge of the subject matter (arithmetic, history, and so on), New York represents the destination – the set of learning objectives that the teacher is expected to help all students achieve by a specific calendar date (such as the end of the school year), and the diverse speeds and routes represent the fact that students come to any class with diverse levels of prior knowledge about the subject matter, different capabilities and limitations with respect to learning, different levels of interest in the topic, and so on. And yet the teacher is still expected to get them all to New York within the same hour.

What does any of this have to do with assessment?

I frequently hear people make statements like this:

“I feel that all this effort on assessment stuff is mostly a huge waste of time and money.”

To borrow a line from the film The Princess Bride:

You keep using that word ["assessment"].  I do not think it means what you think it means. 

When people talk about assessment, they typically seem to be thinking of written tests, and may even have in mind one specific “high-stakes” test. And that is indeed one form of assessment. But assessment, in an educational context, simply means gathering data to figure out where a student is on the map, evaluating where that puts them in relation to the route and schedule, and answering specific questions such as what adjustments to make to keep them on track and on time. 

Assessment can be done with the eyes and ears as well as with a paper test or an electronic GPS-like dashboard. The personal navigator sitting in the car with the student-driver, for example, is constantly assessing the situation using her five senses – looking for road signs, watching what the driver is doing, feeling the acceleration and deceleration of the car, comparing the car’s location against the marked route, and so on. Believe it or not, that’s assessment.  (More specifically, that’s formative assessment.) Another form of assessment is the determination of whether the trip was a success or failure overall – if the child arrives in New York in time for the event, the trip was a success and otherwise it was a failure. (This is an example of summative assessment – in this case, we might call this a “high risk” assessment because the outcome of the assessment correlates with big consequences, for better or worse.)

The fleet navigator (classroom teacher) obviously can’t be in the car with any of the drivers – she has to manage all twenty-five cars for the duration of the trip. But this is 1980, remember – before GPS and cell phones.  So the fleet navigator not only can’t see what every driver is doing inside their cars at any given moment, but she also has no way of tracking precisely where any student’s car is at any given time.  She can’t do anything to help the drivers reach their destination without information about their location and progress – she would effectively be flying blind. Classroom teachers face a very similar challenge - they can't directly observe what's going on in students' heads, and they simply can't teach effectively without good information about where each student is and how they are progressing.

What might we do?

One reasonable strategy would be to set up a series of checkpoints along the main routes.  Drivers check in when they arrive at these checkpoints and that way the fleet navigator can update the map with their approximate locations. If someone fails to check in at the expected time, or if they check in from an alternate location because they cannot find the checkpoint, then the fleet navigator can investigate the problem and decide how to take corrective action to get them back on track.

These checkpoints are analogous to formal educational assessments – including (but certainly not limited to) written tests. The location of a student’s car is analogous to their state of understanding of the subject matter – their progress in the class relative to the curriculum (route) and learning objectives (destination). The checkpoints (formal assessments or tests) help the fleet navigator (classroom teacher) to know much more precisely where each driver (student) is. Importantly, these checkpoints provide early warning – if we have to wait for the child to miss the event in New York (or fail to achieve the learning objectives by the end of the year) to find out if they were on track all along, by then it’s way too late to do anything about it.

The effectiveness of a classroom teacher – like the effectiveness of our fleet navigator – depends critically on the availability of data about individual students.  In addition to the informal assessments teachers are doing constantly using their eyes and ears, formal assessments (including tests) are the checkpoints that provide much of the detailed data about how students are progressing, whether they are on track, and what corrective actions the teacher needs to take.

But why can't teachers just give Friday quizzes and find out all they need to know?

An assessment (quiz, exam, standardized test, etc.) is a measurement instrument - like a ruler, weight scale, or thermometer.  Unlike a ruler, however, which measures things that one can actually see, an assessment is a psychometric ruler - it measures knowledge and skills and other intangible entities of the mind that we can't actually see and that are, in fact, much harder to define than an attribute like length or width. 

Let's ask roughly the same question but in a different domain: "Why do we need to provide engineers and medical doctors with rulers, weight scales, and thermometers to do their work?  Why can't they just create their own to find out all they need to know to do their jobs?"  There are a number of reasons.  Consider calibration, for example. Back in the day people did make and use their own rulers and weights, and they came up with very different measures for the same thing - a major problem if you are paying by the ounce for something, or if you are building a bridge from two ends that should meet in the middle, or if a medical diagnosis depends on the value being measured (body temperature, for instance).

That's not quite the same as the educational scenario, though. Since we can't see the invisible knowledge constructs we are trying to measure in education, we'd have to actually ask "Why can't engineers and medical doctors just create their own measurement instruments while blindfolded and wearing heavy gloves so they can neither see nor feel the thing they are trying to measure?"

Imagine two math teachers in adjacent classrooms each make up their own 10-question math quiz for the same instructional unit.  I've drawn a couple of homemade rulers below to illustrate what that might look like. Obviously, there are major problems with these measurement instruments. Let's consider just a few of the more glaring ones.

Problems with consistency of measurements

Looking at the first ruler, for example, the difference between a score of 1 and 2 is small compared to the difference between a score of 2 vs. 3.  The evenness of the numbers masks underlying unevenness in student understanding, which can lead to invalid educational conclusions and actions.

Problems with interpreting scores

The second ruler is measuring two different dimensions and adding them together. That would be like adding someone's height in feet to their hair length in inches and reporting the resulting number as a score.  How are we to interpret such a score? As a common educational example: when we include printed word problems in our math quiz, a child who struggles with reading may be unable to complete any of them - not because they don't understand the math but because they can't fluently read the problems.  Their score doesn't reflect their math competency - it's a combined math plus reading score. 

Problems with comparing performance across students

Now compare the two rulers.  How are we to compare the performance of students across the two math classes? For example, imagine a student in each class scores a 4 on their version of the quiz.  What can we say about the performance of the two students? They earned the same score - do they have the same math competency? Certainly not. If you look at the length marked by the 4's, then evidently the second student scored about twice as much as the first student. The numbers are not comparable, but they invite interpretation, evaluation, and decision-making as if they mean something specific and comparable.  This is a very real problem that colleges face, for example, when looking at student transcripts.  Looking at two applicants from different states, both having a high school GPA of 3.3, how are the admissions officers to compare them? They really can't.  Love it or hate it, that's one reason the SAT is so widely used - unlike GPA, standardized tests like the SAT provide a common ruler for measuring student competency in specific domains like math and language so the scores can be compared in meaningful ways across students, classes, and schools.

So, is investment in educational assessments a huge waste of time and money?

There is certainly room for healthy debate about whether any particular assessment is valid and fair, how assessments should be administered to students, and how the assessment data should be used. But is it really reasonable to ask whether we can do entirely without educational assessment in schools? Or whether we should really care about the quality and validity of assessment data? Only if it doesn’t really matter what students are learning or when they are actually learning it. But if that’s the case then we have to ask ourselves this: why do we bother sending our children to formal schools with highly trained teachers in the first place? If we really don’t care what they are learning or when, wouldn’t it be better to send them to day care or adventure camp five days each week instead?

In fact, assessment is not a huge waste of time and money.  But without high quality assessment in place to inform effective instruction, large parts of the rest of the educational system might well be.

Postscript: A peek at the future of educational assessment

Now fast-forward from 1980. Imagine a world where teachers have the equivalent of GPS in the classroom - that is, continuous, detailed data on student learning plotted in relation to the curriculum goals, delivered in real-time, and actionable at a glance. Yet students never have to take tests. 

It may sound far-fetched, but it already exists. It's called "embedded assessment" and we've built such a system over at Native Brain to demonstrate conclusively that it's not only technically possible but that it can be made to work at scale in typical public school classrooms - today. (See the screenshot below.)

As I've said before in this blog, we have the know-how right now to make mainstream public school education much, much better than it currently is.  The same way that GPS suddenly transformed the way we drive, technology in the classroom can transform the way teachers teach and the way students learn. There is definitely a way. The question is, do we have the will to make it happen?

(Note: As of the date of this posting the Native Numbers iPad math curriculum and accompanying GPS-like instructional dashboard are currently available at no cost to parents and teachers.)

Check it out. Send us your thoughts. Share.