Learning the Times Tables? Here's How to Do It - Without Tears!

The multiplication facts (or “times tables”). 

They’re important. Kids who don’t know them will struggle later in math.

But many kids resist learning these facts, complaining that they are boring and pointless. And many parents dread them, having had similar experiences as students themselves (and maybe having forgotten their math facts by the time their kids are learning them).

Let’s look at how we can apply a bit of insight from learning science to make the times tables easier to learn and remember.

What’s the problem?

The multiplication facts are usually presented in a table like the one below (the familiar “times table”). We’ll focus on the facts from 1x1 through 10x10 here.

The most common strategy for learning the facts is “brute force memorization” – which means using a combination of worksheets, drills, flashcards and the like to badger the brain into remembering this information through sheer repetition – that is, repeating the same problems over and over again. 

If the brain were like the hard drive on your computer, this might be fine. In fact, we can enter the table of numbers above into a spreadsheet and save it to our computer’s hard disk on the first try – no problem at all.

But we know from brain research that your brain is nothing like the hard drive on your computer. In fact, brute force memorization alone is probably one of the worst possible ways for a human being to learn something.  Brute force memorization can be unpleasant - no wonder kids resist it! – and it’s ineffective.  Even if you manage to hammer the information in there, it’s more likely than not to leak away pretty quickly.

There is a better way

The brain isn’t set up to store large numbers of isolated facts rapidly (like a hard drive).  Instead, it’s set up to identify and encode meaningful patterns. 

What kinds of patterns? Well, visual relationships and symmetry are two good examples. Let’s take a look.

How is the times table constructed?

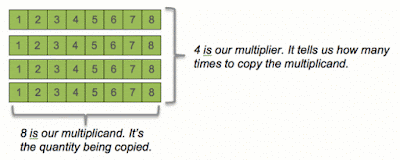
Have you ever thought about where the times table comes from? To understand that, first think about what a multiplication represents. 

If we take a multiplication like 8x4, we are saying we want to copy one number (the multiplicand) a certain number of times (the multiplier).  There’s no hard and fast rule about which order the multiplier and multiplicand are written. For our purposes, consider the first number (8) to be the multiplicand (the number being copied) and the second number (4) to be the multiplier (the number of copies). So in this case “eight times four” means “copy the number eight, four times.”  (Note that the word “multi-ply” is derived from the words for “many layers” – you can see why in the diagram below).

How do we get from the four eights to the result of the multiplication (which is 32)? Easy – just count out the number of squares in the whole rectangle like so…

The familiar times table is made up of all the rectangles representing all the multiplications from 1x1 to 10x10 laid one on top of the other, so that only the very last square of each one - containing the final count of squares in that rectangle - peeks through.  If you look at the cell for the multiplication of interest, you can see that it is at the top, right corner of a rectangle that represents the multiplication of interest (and covers that number of squares).

This visual relationship between the individual multiplication problems and the structure of the whole table can help students understand and remember the facts, because they can start to picture the problems visually in their mind’s eye. Also, if they forget one of the facts, then this conceptual understanding gives them a way to reconstruct it from known facts nearby. 

How can symmetry help students learn the facts?

Consider the multiplication 8x4=32.  This means, “copying eight squares four times gives you thirty-two squares.”  Notice that 4x8=32 means something different, namely “copying four squares eight times gives you thirty-two squares.”  The picture below shows the two visually. 

The rectangles represented by the two multiplications are different shapes, but they give the same result in the end (32 squares).  This works for any two numbers you multiply – changing the order changes the rectangle’s shape but doesn’t change the quantity that results.  This is called the commutative property of multiplication. 

Now let’s apply this insight back to our times table. Look at the table below.  It’s the same as the one above, but color-coded to highlight the symmetry associated with the commutative property. Notice that if you folded the table on its diagonal, the numbers in the two halves would overlap perfectly.

For students, this is great news – it means instead of memorizing all 100 facts, they can learn 55 facts (45 facts in one of the triangles plus the ten facts along the diagonal that are perfect squares like 1x1 or 4x4 – on the diagonal the multiplicand and multiplier are the same and so they have no mirror image).  Learning this one relationship cuts the number of facts almost in half instantly. 

Multiplying by 1: Mono-plying

We can cut the number of facts down further by looking at specific groups of facts.  Multiplying by one, for example, is not really multiplying at all – it’s mono-plying (if multi-ply means “many layers” then mono-ply means “one layer”). 

Remembering the mono-plying rule (multiplying any number by 1 gives you back that same number) takes care of another ten facts, leaving us with just 45 facts to learn.

Multiplying by 10

Multiplying tens is easy, too.  It’s just like multiplying by one except you append a zero to the result.

2x1 = 2 and 2x10 = 20 = “twenty” (derived from the words “twin tens”)
3x1 = 3 and 3x10 = 30 = “thirty”   (derived from the words “three tens”)
4x1 = 4 and 4x10 = 40 = “forty”    (derived from the words “four tens”)
and so on…

To see why, look at the picture.

Adding the rule for multiplying tens takes care of another nine facts, leaving just 36 to learn. 

If 36 multiplication facts still seems like a lot, consider that there are 26 letters in the English alphabet plus ten digits that have names (zero, one, two, etc.), which is also 36 facts.  Your child memorized those, and you can use the same kinds of techniques for the remaining 36 times table facts.  Just keep in mind that helping a child to understand where the facts come from along with patterns like the visual relationships between rectangles and the symmetry that comes from the commutative property will make learning the facts (and other things later, like long multiplication, division, and algebra) much easier.  The knowledge will also stick better and last longer.

Summary

To summarize, we started with 100 multiplication facts to learn, from 1x1 through 10x10. 

First we introduced a few key concepts:

• What is multiplication? It’s copying one number a specified number of times (as in “eight times four” and “times table”) and counting up the quantity that results
• Where does the times table come from? From stacking all the multiplication rectangles on top of one another, letting just the last square of each with the total quantity for that rectangle show through

Then we introduced a few key rules:

• Commutative Property: It doesn’t matter which order you multiply two numbers – it means something different but you still get the same result (Example: 8x4 = 4x8 = 32)
• Multiplying by one (or mono-plying): When you multiply any number by one, you just get that number back
• Multiplying tens: Just like multiplying by one, except you append a zero to the result (Example: 1x4 = 4 and 10x4 = 40). Remember: the name “forty” is just a short form of “four tens”

With these few rules we cut down the number of facts to a manageable 36. Not only does this reduce the memorization load by about two-thirds, but the conceptual understanding will make the remaining facts easier for students to learn and remember.

Additional resources

This is a lot of information (who knew there was so much to know about the lowly times tables?).

Some teachers, tutors, and parents can make use of it in the form it’s presented here in the blog post. To make it easier for everyone else, I’ve packaged this information up into some free videos and a couple of inexpensive apps for iPhone and iPad - each priced less than a pack of index cards. (Note: If you are searching for one of the apps on an iPad, you'll need to change the default filter from "iPad" to "iPhone" apps to find them).

Another great way to help kids learn is to insert yourself into the process – show them you’re interested and available to help if they need it. The same way you read books to your children when they were small, you can sit with them and work through some math mini-lessons at the table, in Minecraft, or using these apps.

Video examples of using Minecraft to learn arithmetic:

• Minecraft Math #1: Numbers - Even, Odd, Prime & Square Root
• Minecraft Math #2: Addition, Multiplication & Commutativity

Bognor’s curse – An Interactive Educational Mini-Adventure

Something’s gone terribly wrong at the Ministry of Magic. The evil wizard Bognor has cast a terrible curse across the land and it’s up to you – a lowly apprentice – to defend your village and defeat his dark magic. To succeed, you’ll have to master some basic Arithmancy. Will you do it?
Watch the video
Experience the magic

Multiplication Explained – Master the Times Tables with Understanding

Multiplication Explained is more than a typical flashcard app. It is a complete mini-curriculum designed to promote both conceptual understanding and fact fluency at the same time.  

Watch the Video
Get the App

Comment and share!
I always love to hear from parents, teachers, and students about ways I can make these resources more useful to help you learn and teach, and what other topics you would like to explore in the blog. 

Educational Assessment: A Huge Waste of Time and Money?

An educational road trip

Imagine it’s 1980 - no World Wide Web, no cell phones, no GPS. Your child is learning to drive a car. They have to drive from Los Angeles to New York in time to attend an important event that could well influence the course of their future life. How would you help them do it? They’d need a long-range plan, of course – a map with a route marked out on it. But this plan alone wouldn’t get them there – they’d need to actively interpret the directions in the real world – identifying which of the many small streets is the right one to turn on, looking for signs and landmarks to know when to change lanes and prepare to exit the highway, constantly checking to make sure they didn’t take a wrong turn, and figuring out how to get back on track when they inevitably do. They must, in other words, constantly be assessing the situation – determining where they are on the map, where that puts them in relation to the route, and what to do at each moment to stay on track and on schedule.

This driving scenario is analogous to formal education. In this case, the subject matter (arithmetic, world history, etc.) is the map. The curriculum is the route marked out on the map. The student is the driver.  The assessment is the process of tracking location and progress in relation to the route, destination, and schedule.

What’s missing from this picture?

If you are a parent, this scenario might make you feel uneasy. Would you really be ok having your child learn to drive while also following a complex and unfamiliar route across thousands of miles over a number of days with important consequences riding on their timely arrival? (Analogously, would you expect that your child would buckle down and successfully learn to read books or master algebra on their own by June, given that they want to be a writer, carpenter, engineer, doctor, or architect when they grow up?) Probably not. If they had to make the trip by car and they had to do the driving, you’d probably want to send someone along with them – a navigator and guide who knows the route well, can coach them on how to drive safely and skillfully, and looks after their well-being during the trip - making sure they leave on time each morning, get plenty of sleep, and don’t get lost or sidetracked visiting roadside attractions along the way.

In the educational analogy, the navigator is the educational guide.  But not a classroom teacher – this navigator is a personal tutor working with one student.

Imagine that we cannot afford to provide a navigator (personal tutor) for each driver, but that we can allocate one navigator for each fleet of twenty-five cars. These cars are all leaving from different starting cities, at different times, moving at different speeds, with drivers who have different levels of driving experience and skill, and different levels of familiarity with their route.  Nonetheless, the fleet navigator is responsible for seeing that all drivers arrive in New York within the same hour.

In the educational analogy, the fleet navigator is the classroom teacher.  The cities the students start in are their prior knowledge of the subject matter (arithmetic, history, and so on), New York represents the destination – the set of learning objectives that the teacher is expected to help all students achieve by a specific calendar date (such as the end of the school year), and the diverse speeds and routes represent the fact that students come to any class with diverse levels of prior knowledge about the subject matter, different capabilities and limitations with respect to learning, different levels of interest in the topic, and so on. And yet the teacher is still expected to get them all to New York within the same hour.

What does any of this have to do with assessment?

I frequently hear people make statements like this:

“I feel that all this effort on assessment stuff is mostly a huge waste of time and money.”

To borrow a line from the film The Princess Bride:

You keep using that word ["assessment"].  I do not think it means what you think it means. 

When people talk about assessment, they typically seem to be thinking of written tests, and may even have in mind one specific “high-stakes” test. And that is indeed one form of assessment. But assessment, in an educational context, simply means gathering data to figure out where a student is on the map, evaluating where that puts them in relation to the route and schedule, and answering specific questions such as what adjustments to make to keep them on track and on time. 

Assessment can be done with the eyes and ears as well as with a paper test or an electronic GPS-like dashboard. The personal navigator sitting in the car with the student-driver, for example, is constantly assessing the situation using her five senses – looking for road signs, watching what the driver is doing, feeling the acceleration and deceleration of the car, comparing the car’s location against the marked route, and so on. Believe it or not, that’s assessment.  (More specifically, that’s formative assessment.) Another form of assessment is the determination of whether the trip was a success or failure overall – if the child arrives in New York in time for the event, the trip was a success and otherwise it was a failure. (This is an example of summative assessment – in this case, we might call this a “high risk” assessment because the outcome of the assessment correlates with big consequences, for better or worse.)

The fleet navigator (classroom teacher) obviously can’t be in the car with any of the drivers – she has to manage all twenty-five cars for the duration of the trip. But this is 1980, remember – before GPS and cell phones.  So the fleet navigator not only can’t see what every driver is doing inside their cars at any given moment, but she also has no way of tracking precisely where any student’s car is at any given time.  She can’t do anything to help the drivers reach their destination without information about their location and progress – she would effectively be flying blind. Classroom teachers face a very similar challenge - they can't directly observe what's going on in students' heads, and they simply can't teach effectively without good information about where each student is and how they are progressing.

What might we do?

One reasonable strategy would be to set up a series of checkpoints along the main routes.  Drivers check in when they arrive at these checkpoints and that way the fleet navigator can update the map with their approximate locations. If someone fails to check in at the expected time, or if they check in from an alternate location because they cannot find the checkpoint, then the fleet navigator can investigate the problem and decide how to take corrective action to get them back on track.

These checkpoints are analogous to formal educational assessments – including (but certainly not limited to) written tests. The location of a student’s car is analogous to their state of understanding of the subject matter – their progress in the class relative to the curriculum (route) and learning objectives (destination). The checkpoints (formal assessments or tests) help the fleet navigator (classroom teacher) to know much more precisely where each driver (student) is. Importantly, these checkpoints provide early warning – if we have to wait for the child to miss the event in New York (or fail to achieve the learning objectives by the end of the year) to find out if they were on track all along, by then it’s way too late to do anything about it.

The effectiveness of a classroom teacher – like the effectiveness of our fleet navigator – depends critically on the availability of data about individual students.  In addition to the informal assessments teachers are doing constantly using their eyes and ears, formal assessments (including tests) are the checkpoints that provide much of the detailed data about how students are progressing, whether they are on track, and what corrective actions the teacher needs to take.

But why can't teachers just give Friday quizzes and find out all they need to know?

An assessment (quiz, exam, standardized test, etc.) is a measurement instrument - like a ruler, weight scale, or thermometer.  Unlike a ruler, however, which measures things that one can actually see, an assessment is a psychometric ruler - it measures knowledge and skills and other intangible entities of the mind that we can't actually see and that are, in fact, much harder to define than an attribute like length or width. 

Let's ask roughly the same question but in a different domain: "Why do we need to provide engineers and medical doctors with rulers, weight scales, and thermometers to do their work?  Why can't they just create their own to find out all they need to know to do their jobs?"  There are a number of reasons.  Consider calibration, for example. Back in the day people did make and use their own rulers and weights, and they came up with very different measures for the same thing - a major problem if you are paying by the ounce for something, or if you are building a bridge from two ends that should meet in the middle, or if a medical diagnosis depends on the value being measured (body temperature, for instance).

That's not quite the same as the educational scenario, though. Since we can't see the invisible knowledge constructs we are trying to measure in education, we'd have to actually ask "Why can't engineers and medical doctors just create their own measurement instruments while blindfolded and wearing heavy gloves so they can neither see nor feel the thing they are trying to measure?"

Imagine two math teachers in adjacent classrooms each make up their own 10-question math quiz for the same instructional unit.  I've drawn a couple of homemade rulers below to illustrate what that might look like. Obviously, there are major problems with these measurement instruments. Let's consider just a few of the more glaring ones.

Problems with consistency of measurements

Looking at the first ruler, for example, the difference between a score of 1 and 2 is small compared to the difference between a score of 2 vs. 3.  The evenness of the numbers masks underlying unevenness in student understanding, which can lead to invalid educational conclusions and actions.

Problems with interpreting scores

The second ruler is measuring two different dimensions and adding them together. That would be like adding someone's height in feet to their hair length in inches and reporting the resulting number as a score.  How are we to interpret such a score? As a common educational example: when we include printed word problems in our math quiz, a child who struggles with reading may be unable to complete any of them - not because they don't understand the math but because they can't fluently read the problems.  Their score doesn't reflect their math competency - it's a combined math plus reading score. 

Problems with comparing performance across students

Now compare the two rulers.  How are we to compare the performance of students across the two math classes? For example, imagine a student in each class scores a 4 on their version of the quiz.  What can we say about the performance of the two students? They earned the same score - do they have the same math competency? Certainly not. If you look at the length marked by the 4's, then evidently the second student scored about twice as much as the first student. The numbers are not comparable, but they invite interpretation, evaluation, and decision-making as if they mean something specific and comparable.  This is a very real problem that colleges face, for example, when looking at student transcripts.  Looking at two applicants from different states, both having a high school GPA of 3.3, how are the admissions officers to compare them? They really can't.  Love it or hate it, that's one reason the SAT is so widely used - unlike GPA, standardized tests like the SAT provide a common ruler for measuring student competency in specific domains like math and language so the scores can be compared in meaningful ways across students, classes, and schools.

So, is investment in educational assessments a huge waste of time and money?

There is certainly room for healthy debate about whether any particular assessment is valid and fair, how assessments should be administered to students, and how the assessment data should be used. But is it really reasonable to ask whether we can do entirely without educational assessment in schools? Or whether we should really care about the quality and validity of assessment data? Only if it doesn’t really matter what students are learning or when they are actually learning it. But if that’s the case then we have to ask ourselves this: why do we bother sending our children to formal schools with highly trained teachers in the first place? If we really don’t care what they are learning or when, wouldn’t it be better to send them to day care or adventure camp five days each week instead?

In fact, assessment is not a huge waste of time and money.  But without high quality assessment in place to inform effective instruction, large parts of the rest of the educational system might well be.

Postscript: A peek at the future of educational assessment

Now fast-forward from 1980. Imagine a world where teachers have the equivalent of GPS in the classroom - that is, continuous, detailed data on student learning plotted in relation to the curriculum goals, delivered in real-time, and actionable at a glance. Yet students never have to take tests. 

It may sound far-fetched, but it already exists. It's called "embedded assessment" and we've built such a system over at Native Brain to demonstrate conclusively that it's not only technically possible but that it can be made to work at scale in typical public school classrooms - today. (See the screenshot below.)

As I've said before in this blog, we have the know-how right now to make mainstream public school education much, much better than it currently is.  The same way that GPS suddenly transformed the way we drive, technology in the classroom can transform the way teachers teach and the way students learn. There is definitely a way. The question is, do we have the will to make it happen?

(Note: As of the date of this posting the Native Numbers iPad math curriculum and accompanying GPS-like instructional dashboard are currently available at no cost to parents and teachers.)

Check it out. Send us your thoughts. Share.

Minecraft Scientists Ep. #1: Fishin' In the Rain (STEM Education)

Minecraft might be the ultimate tool for STEM education (Science, Technology, Engineering, and Mathematics).  Check it out...

(Want to try the experiment yourself? Get instructions in the spreadsheet linked below.)

What Is Science?
Science – experimental science in particular – is like a game of 20 questions we play with Mother Nature. We have a question like “Am I more likely to catch fish on rainy days than on clear days (or does it make a difference)?” Maybe no human being knows the answer, but Mother Nature does. 

Only she isn’t going to just tell us the answer straight up – she doesn’t speak English, after all. We have to be more clever in how we get the answers from her. 

The Scientific Method
One thing we can do is make a guess (form a hypothesis), and then submit the guess to her (run an experiment).  For example, for the question about when you are likely to catch more fish, we might run an experiment like this: go to the same exact fishing spot each day for 10 clear days and 10 rainy days, always arriving and leaving at the same time of day, always using the same rod and tackle, and always using the same bait. (We call this “controlling” for location, time of day, total fishing time, equipment, and bait, and we do it to make sure that it’s the weather and not some other factor like the particular bait we use that is causing any differences in how many fish we catch each day.)

The data we get from the experiment (the number of fish we catch on 10 clear days and 10 rainy days) is Mother Nature’s answer to one of our questions, and it might range from “yes” to “probably yes” to “maybe” to “probably no” to “no” to “no comment.”  (Also: we usually have to analyze the raw data in some way to find out what her answer actually is.) Through playing this game of 20 questions with Mother Nature and pulling together all of the clues we get from our experiments we can get more precise and certain answers to our questions over time. 

21st Century Science Education: Real Science in a Virtual World
The best (and most fun) way of really learning science is by doing real experiments like the 20-day fishing experiment described above. But real experiments like this one often require a lot of money and time, and so we can’t really do that for every kid.  

Or can we? The video shows an example of doing real science in the virtual world of Minecraft a lot faster and less expensively than we could in the real world - and without having to get wet! 

File this under “things I wish they had when we were in school.” 

Science Can Surprise Us!
Swifty7777 and I have run the experiment once (collecting 20 Minecraft days’ worth of data between the two of us – less than an hour of real time) – and, as often happens in science, we were surprised by what we found.  In fact, our results seem to contradict what the Minecraft wiki says is true - they indicate you should catch about 20% more fish in the rain than on a clear day. (Watch the video for details on what we found.)

Who is right – us or the Minecraft wiki?

Your Turn! Try the Experiment Yourself
You can help us figure it out: replicate our experiment (that means run it again the same way – just like real scientists do!) and see if you get the same results. 

Besides, if you really want to learn science, you have to do more than watch videos of other people doing it - you have to get in there and work through it yourself.  We've provided an Excel spreadsheet for you to download here that makes it easy for you to do that.

If you email your filled out spreadsheet to info@i4kd.com with the subject line “Minecraft Fishing Experiment #1”, we’ll post your results so people can compare them to ours.

Happy fishing!

Epic_MC_Player and Swifty7777
// The Minecraft Scientists


Instructions for running the experiment yourself are here (same as link above).

If you liked this "learning with Minecraft" video, you might also like these:
Minecraft Math #1: Numbers - Even, Odd, Prime & Square Root
Minecraft Math #2: Addition, Multiplication & Commutativity

Common Core Math Standards Making You Crazy? Some Things to Consider

Pop Quiz!

(No Googling or peeking at other people's answers before responding, please - this is a closed-book quiz. Also: this will not go on your permanent record.)

With reference to the long multiplication problem above, please answer the following questions.

Q1) What does the "4" that is circled mean?

Q2) What does that zero in the second row mean (the one that is circled)?

We'll come back to this later.

Common Core Math Standards: What's the Point?

Our topic today is the Common Core Math Standards.  They seem to have some people in a tizzy.

The picture at left, for example, has been making the rounds on the internet. Evidently someone snapped this picture of their child's math homework because they were enraged by it, and lots of people are hopping on the bandwagon.

This is curious to me.

The intent here should be pretty clear - the point is to develop the child's conceptual understanding of subtraction. This happens in parallel to developing their fluency in the standard subtraction algorithm that we all learned as children (not shown on this page, but also covered in the Common Core standards).  The standard subtraction algorithm is efficient for calculating, but doesn't support understanding.

Do We Really Need to Change the Way We Teach Math?

Why would we want to teach a child to understand the concepts behind the algorithms?  Isn't that just a waste of time?  We all did fine just learning the algorithms by rote, didn't we?

Well, no.  It turns out adults in the U.S. aren't very good at math.

Speaking of which - let's take a moment to reflect on the quiz above.  How did you do on it? How quickly could you answer? Did you step away to search the internet for some clues or look at the poll results before submitting your own answers? (Naughty monkey!) How confident were you in your responses?

The simple fact is we are failing our kids in math education, and we have been for generations.  Here are some more fun facts to illustrate the point:

• According to the National Assessment of Educational Progress, only about two in five U.S. 4th graders are proficient in math.  That drops to about one in three students by 8th grade.
• According to the Programme for International Student Assessment, the U.S. ranks below the international average on tests of mathematics.  This is despite the fact that the U.S. spends more per pupil than other countries.

It's pretty clear we're doing something wrong. Solving big problems like this requires big changes.

How Can We Do Better?

If we look at some of the top performing countries, like Singapore, and ask what they are doing that we aren't, the most obvious difference is that they focus on conceptual understanding a whole lot more than we do, and they spend a lot less time teaching things by rote.  They teach the kids several models and methods for thinking about numbers and operations on numbers, for example - methods like the "Counting Up" method represented in the picture above. It's not a secret. We have just stubbornly refused to do it (until recently, anyway, with the arrival of the Common Core math standards).

But Aren't We Just Complicating Things?

Teaching concepts may take more time than memorizing a few recipes for calculating without understanding (at least initially), and some people seem to object to spending the extra time.  

This is extremely short-sighted.  There may be more time spent initially developing understanding, but that investment will pay dividends many times over across the student's time in school, from kindergarten through high school (and beyond).  Understanding the concepts makes later learning far more efficient - and effective. By spending more time developing foundational understanding, we could actually get better outcomes while spending less time on the math curriculum overall. Not only that, but students who understand what's going on have a much better experience, are more engaged, and are more confident. All good.

Why Can't We Just Do What We've Always Done?

What does it look like when we fail to teach children conceptual understanding?  The video below shows one example of a second grader working on some grade-level math problems.

Notice that she knows the numbers and she knows how to count - these are typically learned by rote. Her conceptual understanding is very weak, however, and as a result she has to go through a laborious process of counting up from zero to answer simple questions like "How much do I have if I add 10 to 35?"  And then she gets the wrong answer. Repeatedly.

Time invested in developing authentic understanding is not a waste of time.  Quite the contrary. The real waste is time spent teaching without developing understanding - which produces the kind of disjointed, brittle, and tentative knowledge shown in the video - which is ultimately quite useless and will likely fade away rapidly.

This is all too common.  This could well be any of our children.  The maddening thing is that there's every reason to believe this child - and virtually every child - is completely capable of understanding the concepts she would need to reason fluently about the questions being asked of her in this video. She's not failing at math. Our education system is failing her. The same way it has failed generations before her.  In large part by teaching math by rote, without conceptual understanding. (Don't scapegoat the teachers, by the way - the root problems here are systemic.)

We could try to press ahead as some people are advocating and just teach this child the algorithms for long addition, multiplication, and division as we have always done.  But with such a weak foundation of understanding, what would we really expect to achieve that way? Her performance on those would quickly come to look like her performance here - labored, uncertain, and error-prone. Eventually she could well stop using the algorithms for lack of confidence, or even forget them altogether.

This is the sort of large scale, systemic problem the Common Core Math Standards are meant to rectify.

Could the explanation in the textbook shown in the picture above be edited for clarity?  Sure it could.

Is that evidence that the Common Core is a failure and should be trashed?  Far from it. We've been doing math education wrong for a very long time. The Common Core Math Standards represent a big step in the right direction - in the direction of what Singapore and other top-performing countries do, in fact.

Some people seem to think the textbook image above is crazy. What's really crazy is recognizing that the status quo is not acceptable while repeating the same educational processes generation after generation and expecting a better result.

Come to think of it, wasn't that literally Einstein's definition of insanity?

Celebrating Howard Gardner's Extraordinary Mind, Life, and Work (with a free book download)

Howard Gardner is the Hobbs Professor of Cognition and Education at the Harvard Graduate School of Education.


Howard Gardner has been identified by Foreign Policy and Prospect magazines as one of the 100 most important public intellectuals in the world today.  His work has fundamentally changed the way many people (and institutions) think about intelligence (with his theory of Multiple Intelligences), creativity, and education (to name just a few of the areas he has touched).

Happy Birthday, Howard!

Howard turned 70 last year.  To celebrate, his wife (Ellen Winner) and one of his former students (Mindy Kornhaber) hosted a Festschrift in his honor.  (A Festschrift – derived from the German for ‘celebration writing’ – is a collection of writings published in honor of a scholar.) They invited Howard’s teachers, peers, colleagues, and former students to contribute essays inspired by his work and his relationships with them.  One hundred and sixteen of Howard’s close colleagues contributed to the two-volume work, entitled Mind, Work, and Life: A Festschrift on the Occasion of Howard Gardner’s 70th Birthday. Each contribution includes a personal note from the contributor and a personal response from Howard.  Running 605 pages in length, this is quite a remarkable work, providing a unique and intimate portrait of this extraordinary man and his profound influence on some of the people who have worked most closely with him.

Mind, Life, and Work: A Festschrift on the Occasion of Howard Gardner's 70th Birthday

The complete two-volume Festschrift is available for free download as a PDF here, or if you prefer physical books you can buy it at cost from Amazon here.  Other options, including kindle versions of the two volumes, are listed here.

My contribution (starting on p. 223) is entitled, There’s More Than One Way to Bridge a Gap: On the Promise of Computational Neuroscience for Education.  I wrote it as a doctoral student in Education, soon after I took my first class with Howard.  At the time, I was just beginning to wrestle in earnest with the question: “How can scientific insights about the brain and mind help us make education better?”  As reflected in this essay, Howard’s teaching was instrumental in helping me frame the key issues in a new and more productive way, which I have continued to build on to this day.  If you are interested in the relationship between the brain and mind, or in how we might go about leveraging insights about the biology of learning to improve educational practice, you might find it interesting.  I look forward to reading your comments on that or anything else in the book.

Enjoy!

Teacher Appreciation Week: A Personal Tribute to Teachers

It’s easy to see and criticize the flaws in our education system here in the U.S. – especially our public education system. And teachers are the face of public education – which means they often take the brunt of the criticism and discontent from all quarters, even for issues completely beyond their control.

Teacher Appreciation Week is a time to pause and reflect on the good and important work that teachers do – and to openly express our gratitude to these people who have dedicated their lives to helping our children (and us, when we were children ourselves) become happy and productive members of society.

I am a product of public education. I can only imagine what my life would have been like if I had been born into a society without it. And I can only imagine what my school experience – and my life – would have been like without the benefit of the extraordinary courage, kindness, and skillful teaching exhibited by many individual teachers I had the good fortune to meet along the way.

Carole Rosen-Kaplan, for example, was my 11th grade English teacher. She became a dear friend. Sadly, she passed away recently. Carole’s sons asked me to provide some comments for her memorial service. I realize now – too late – that although we talked a couple of times a year, I never told her how much I appreciated her as a teacher, or what a profound impact her teaching had on my life. I regret that.

I’m trying to make up for it a bit by “paying it forward.” Teaching is extraordinarily hard work. Often it’s thankless. Sharing the comments below is my way of saying to all of you, teachers:
Thank you.
I appreciate what you do.
The work you do influences and transforms your students’ lives in ways you (and they) will probably never know.

 ***

I met Carole when I was a high school junior. Her English Composition class wasn’t the English elective I wanted that year, but it was the only one that fit my schedule.

In retrospect, the class was so thoughtfully crafted and compelling that even today (decades later) I could probably write down most of the syllabus from memory.

I wrote my first short story for that class. It was about an archaeologist who stumbles upon a powerful relic in Egypt and uses it to travel back in time but ends up trapped. Carole (Mrs. Rosen-Kaplan to me then) asked me if I plagiarized it. I thought “Wow, that must be a pretty good story.” I don’t think it was her intent in that moment, but that honest exchange started me thinking that if I could accidentally make an English Composition teacher believe I had stolen a published story then maybe I could be a real writer who actually published stories. (Inspiration takes many forms.)

I wrote several chapters of a novel that year (which she read and commented on in her own time), and later became president of the school’s Creative Writing Club - my first formal leadership role. One of my short stories won a prize in a writing competition. I later wrote a short story for my college essay. It worked! (I got in.) AND a love poem for a woman. It also worked! (She’s my wife.)

It turns out that English Composition is crazy powerful stuff.

That year I argued against nuclear stockpiling in a mock trial of the global superpowers and wrote passionately about the Vietnam war, the Holocaust, and human slavery.

The class *involved* writing but it wasn’t *about* writing. It was about love and hate, good and evil, right and wrong, politics and power.

As I reflect back on the class now, though, I realize that what is remarkable to me about Carole’s teaching is that we didn’t simply *read* other people’s thoughts on these themes or even write about them in the abstract. When writing for Carole we had to choose sides - we had to “try on” different points of view and in the end commit to one. On the theme of War: will you, as the author of this essay, choose to glorify or vilify it?

More importantly - on the subject of war: will you, as the author of your own life, choose to glorify or vilify it?

But helping us find our voice was only one of Carole’s objectives. Her other objective was to impress upon us our responsibility to use it.

Perhaps the most poignant statement of individual responsibility I have ever read is captured in these lines by Martin Niemöller (assigned in Carole's class) about the Nazi purges:

First they came for the Socialists, and I did not speak out – Because I was not a Socialist. 
Then they came for the Trade Unionists, and I did not speak out – Because I was not a Trade Unionist. 
Then they came for the Jews, and I did not speak out – Because I was not a Jew. 
Then they came for me – and there was no one left to speak for me. 

I have recalled this passage to mind many times over the decades. It reminds me of my right - and my responsibility - to use my voice. More importantly, it reminds me that sometimes doing the right thing is deeply uncomfortable all around - and that courage does not mean the absence of fear but rather doing the right thing in the face of fear. Speaking up and speaking out is not the responsibility of a chosen few - it is the right and responsibility of every human being.

Carole’s class was called “English Composition” but the full title should have been something like English Composition: How to Find Your Voice and Raise Hell Through Writing.

I think Carole saw promise in me as her 11th grade English Composition student and was disappointed that in the end she didn’t inspire me to pursue a creative writing career.

But here is what I would say to her in response to that…

Carole,
Thanks in part to you I know who I am and who I aspire to become. I know what I stand for. I stand for what is right, what is true, what is just, and what is good. I stand for people - especially the people who can’t stand for themselves, like children. I stand for the right of every human being to discover their own voice and have the opportunity to be heard. I stand for the importance of helping people discover who they are, who they want to become, what they are deeply passionate about, and how to become the authors of their own lives.

No, you didn’t inspire me to become a creative writer.

You inspired me to become an Educator.  Like you.

All my love,
-Mike Connell
April 26, 2014

Mind the Quicksand: A Word of Warning to EdTech Investors

I read about a new EdTech startup this morning in TechCrunch. It's called Galxyz. I started writing a comment on the article page itself, but then it got really long and kind of "meta." So I thought it might make an interesting blog post.

Here's the description of the company from TechCrunch:

Galxyz (it’s pronounced “galaxies”, and it’s a nightmare to spell) is building a science-focused game for tablets and smartphones. And the company really is just focused on one game — Rashid [the founder] described it as “an intergalactic science adventure,” one that kids could potentially play for years, battling a villain called King Dullard across the galaxies. As they do so, they’re also learning about science at their own pace.

You can check out their epic promo video here (I would embed it, but that might violate copyright).

Sounds interesting enough.  Although an antagonist called "King Dullard" is a little on-the-nose, if you know what I mean.

What's the new angle on education, I wondered?

Apparently the idea came to Rashid as he saw his own children playing educational games, which he found lacking in several ways. He said they weren’t engaging enough, the content wasn’t deep enough, or they required the parents to get involved in order for the kids to advance. That second point is why he’s focusing on a single title — so that kids can just keep playing rather than running out of material after a few weeks.

Wow - it seems so obvious once he points it out.  I wonder why this hasn't occurred to anyone before? 

Anyone who follows this blog knows that I believe it is entirely possible to make education orders of magnitude better.  And that I applaud any authentic effort to try.

But from where I stand, this has "Titanic" written all over it.  

I am confident that producing truly effective education at scale is harder than any business or engineering challenge the good people at Galxyz have ever faced.  

This isn't about them, though.  I wish them well.  For purposes of this blog post, they represent just the latest in an endless parade of investor-backed EdTech entrepreneurs who seem to have almost exactly the same creation story.  I'm not upset about it.  I'm more intrigued.

One aspect of education that fascinates me is that to outsiders it always looks so *simple*.

As simple as running across that wet, sandy patch of ground in the jungle to get to a fabulous treasure twenty feet away.  But wait...it's hard to believe no one has run over there and taken that treasure before...hmmm...don't you wonder why? (Hint: That's not sand.)

What follows is my prediction for this venture.  

To be clear, this is not what I wish for them.  I want truly better education more than just about anything, and I'm indifferent as to whether it comes from a for-profit or non-profit venture, as long as we get it.  And it's so close I can almost taste it.  

The prediction is based on a pattern that I see play out over and over and over and over and over again (that's right - five 'overs').  

It looks like this...

Day 1: Outlook bright, mattress so overflowing with cash I can't climb onto it so am sleeping on the couch, burn rate 7, feeling great, gonna make history and be a hero by fixing education because I'm...
(Choose all that apply)

• A product of an education system, and therefore I know how to educate...more better...than anyone
• More funner than anyone in education today
• In possession of more revolutionary technology than those other people
• More smarter
• Mo' richer
• A bit confused about the difference between money, intelligence, and expertise

Day 30: Epic teaser promo video produced, first prototype created and friends (who are also employees, or hoping to be) are saying it's definitely the next big thing - time to pick up the pace of hiring animators, writers, and engineers!  Mattress so overstuffed with clams that I rolled off it last night.  (Ouch.)  Outlook blazing, increasing burn rate to 9.0.

Day 180: A bunch more concepts storyboarded and prototyped, things seem to be moving right along.  Still, things are getting a bit confusing.  We discovered that narratives are inherently linear and learning appears to be inherently nonlinear, so that's creating some "design challenges" (so-called).  Can the kids go through the same narrative ten times if that's what they need in order to understand the concept?  But wait - even if they will tolerate that, isn't one definition of insanity "doing the same thing over and over while expecting a different result"?  Should we have multiple narratives for each concept? Wow - that would be expensive.  Let's stick with the one narrative.  Should we at least present each concept in multiple different ways to help kids understand it? But will all those choices confuse them?  And what other ways are there to present the concepts within a single narrative? This is taking longer than we thought - better hire more animators and engineers!  Mattress slightly overstuffed with cabbage. Burn rate goes to 11. Outlook bright.

Day 240: Somehow a couple of teachers got wind of what we were doing and we invited them in for a demo.  They were really harshing on our mellow.  They think the whimsical five minute cut scenes between short sets of learning activities are too long - complaining about how that's going to "steal learning time" or something.  But don't they understand that's what makes learning fun?!  (And how many simoleons we have invested in those videos?!)  They also wanted to know what kinds of student performance data we are going to provide.  We showed them the awesome score meter and the leaderboards but they didn't seem to get it.  That's why we didn't want to bring any teachers up in here - we just knew they wouldn't understand our Vision.  Mattress still stuffed with ample Benjamins. Burn rate holding steady at 11.

Day 330: Brought some kids in to play test for the first time.  They thought the narrative was kind of hokey and felt tacked on to the learning activities.  Lenny's kid called it "chocolate covered broccoli."  That's why I didn't want to bring students up in here - we just knew they wouldn't understand our Vision. The writers and animators are getting a little up in arms because people keep changing requirements and trying to mess with their narrative.  I sympathize with them - the narrative is the hard and expensive part, so shouldn't we revise the science material to fit it instead of the other way around?  Running a bit behind schedule.  Mattress feeling a bit lumpy.  Better pull back on contractors to conserve cash.  Burn rate reduced to 8.

You can imagine where it goes from here - the way of 38 Studios or a quick exit that amounts to a soft crash landing.  Like I said - quicksand.  The pattern is that they don't discover where the real complexities in education lie until they are in it up to their necks.

Here's some unsolicited advice for engineers and investors who are eyeing EdTech:

• If you think you can crack the code on better education with money, you are wrong
• If you think you can crack the code on better education with raw intelligence, you are wrong
• If you think the core challenges in EdTech are technical, you are wrong
• If you think the silver bullet is in "making learning fun" or "engaging" students, you are wrong
• If you think the solution is in making clever lessons for each concept, you are wrong
• If you think you can solve this problem with better graphics, animation, and narrative, you are wrong
• If you think bringing even all of the above elements to the table *must* be sufficient to crack the code on better education, you are still wrong - though you might be able to generate a positive ROI that way.  Or not.

Relay Ventures, Andreessen Horowitz, and Emerson Collective (the investors backing Galxyz) - you are welcome to use the above as a litmus test when evaluating EdTech pitches in the future.  (Acknowledgement as the source is always appreciated.)

Don't get me wrong: I strongly believe there is a path to better education.  This just isn't it.

I can hear the incredulous guffaws now.  We are on Day 30 and the outlook is blazing - we have an epic promo video and the prize is practically within reach!

I don't really see any point in debating the matter right now - this is a prediction, not a challenge.  Let's check back in a year and see where things stand.  I would be pleasantly surprised to be wrong.  But I wouldn't bet on it.